PyTorch 教程：从头开始构建一个简单的神经网络Neural Networks

本文最后由 Demo Marco 更新于 2025-02-22. 如有资源已失效，请留言反馈，将会及时处理。 【推荐：不翻墙访问被墙网站方法 | 自用高速专线机场 | 高速CN2线路 | 高质量家宽住宅IP】

在本 PyTorch 教程中，我们将介绍驱动神经网络的核心函数，并从头开始构建自己的神经网络。本文的主要目的是演示 PyTorch（一个优化的深度学习张量库）的基础知识，同时为您提供有关神经网络工作原理的详细背景。 

什么是神经网络？ 

神经网络也被称为人工神经网络 (ANN)。该架构构成了深度学习的基础，而深度学习只是机器学习的一个子集，其算法灵感来源于人类大脑的结构和功能。简而言之，神经网络构成了模仿生物神经元相互发送信号的架构的基础。 

因此，你经常会发现一些资源会花费前五分钟绘制出人脑的神经结构，以帮助你直观地了解神经网络的工作方式。但是，当你没有多余的五分钟时，将神经网络定义为将输入映射到所需输出的函数会更容易。 

通用神经网络架构包括以下内容：

• 输入层：数据通过输入层输入网络。输入层中的神经元数量等于数据中的特征数量。从技术上讲，输入层不被视为网络中的层之一，因为此时不发生任何计算。 
• 隐藏层：输入层和输出层之间的层称为隐藏层。网络可以有任意数量的隐藏层 – 隐藏层越多，网络越复杂。 
• 输出层：输出层用于进行预测。 
• 神经元：每一层都有一组与其他层的神经元相互作用的神经元。 
• 激活函数：执行非线性转换，帮助模型从数据中学习复杂的模式。 

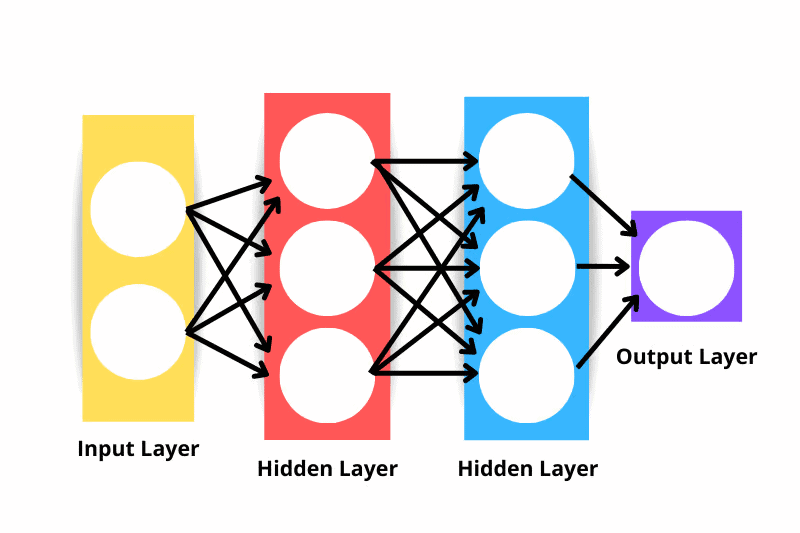
请注意，上图显示的神经网络将被视为三层神经网络，而不是四层神经网络 – 这是因为我们没有将输入层作为层。因此，网络中的层数是隐藏层的数量加上输出层的数量。

神经网络如何工作？ 

让我们将算法分解为更小的部分，以便更好地理解神经网络的工作原理。

权重初始化

权重初始化是神经网络架构中的第一个组件。我们设置的初始权重定义了神经网络模型优化过程的起点。 

如何设置权重很重要，尤其是在构建深度网络时。这是因为深度网络更容易受到梯度爆炸或梯度消失问题的影响。梯度消失和梯度爆炸问题超出了本文的范围，但它们都描述了算法无法学习的情况。 

虽然权重初始化不能完全解决梯度消失或爆炸问题，但它确实有助于预防梯度消失或爆炸问题。 

以下是一些常见的权重初始化方法： 

零初始化

零初始化意味着权重被初始化为零。这不是一个好的解决方案，因为我们的神经网络无法打破对称性——它不会学习。 

每当使用常数值初始化神经网络的权重时，我们都可以预期它的表现会很差，因为所有层都会学习相同的东西。如果所有隐藏单元的输出对成本的影响都相同，那么梯度就会相同。 

随机初始化

随机初始化打破了对称性，这意味着它比零初始化更好，但有些因素可能会决定模型的整体质量。 

例如，如果权重随机初始化为较大的值，那么我们可以预期每次矩阵乘法都会产生一个明显较大的值。在这种情况下应用 S 型激活函数时，结果会接近 1，这会减慢学习速度。

随机初始化可能导致问题的另一种情况是，如果权重被随机初始化为较小的值。在这种情况下，每次矩阵乘法都会产生明显较小的值，而应用 S 型函数将输出更接近零的值，这也会减慢学习速度。 

Xavier/Glorot 初始化 

Xavier 或 Glorot 初始化（无论哪个名字）是一种用于初始化权重的启发式方法。每当将 tanh 或 sigmoid 激活函数应用于加权平均值时，通常都会看到这种初始化方法。该方法最早是在 2010 年由 Xavier Glorot 和 Yoshua Bengio 在题为《理解训练深度前馈神经网络的难度》的研究论文中提出的。这种初始化技术旨在保持整个网络的方差相等，以防止梯度爆炸或消失。 

He/Kaiming 初始化 

He 或 Kaiming 初始化是另一种启发式方法。与 He 和 Xavier 启发式方法的不同之处在于，He 初始化对考虑激活函数非线性的权重使用了不同的缩放因子。 

因此，当在层中使用 ReLU 激活函数时，建议使用 He 初始化方法。您可以在He 等人撰写的《深入探究整流器：在 ImageNet 分类上超越人类水平的表现》中了解有关此方法的更多信息。

前向传播

神经网络的工作原理是取加权平均值加上偏差项，然后应用激活函数来添加非线性变换。在加权平均公式中，每个权重决定每个特征的重要性（即它对预测输出的贡献程度）。

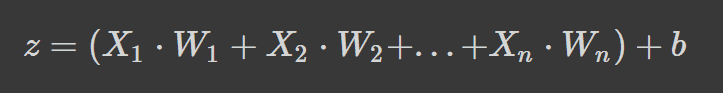
上面的公式是加权平均值加上偏差项，其中， 

• z 是神经元输入的加权和
• Wn 表示权重
• Xn 表示独立变量，
• b 是偏差项。

如果这个公式看起来很熟悉，那是因为它是线性回归。如果不将非线性引入神经元，我们将得到线性回归，这是一个简单的模型。非线性变换使我们的神经网络能够学习复杂的模式。 

激活函数

我们已经在权重初始化部分提到了一些激活函数，但现在您知道它们在神经网络架构中的重要性。

让我们深入探讨您在阅读研究论文和其他人的代码时可能会看到的一些常见激活函数。  

乙状结肠

S 型函数的特点是曲线呈“S”形，介于 0 和 1 之间。它是一个可微分函数，这意味着曲线的斜率可以在任意两点找到，并且是单调的，这意味着它既不会完全增加也不会完全减少。您通常会将 S 型激活函数用于二元分类问题。

下面展示了如何使用 Python 来可视化你自己的 S 型函数： 

# Sigmoid function in Python
import matplotlib.pyplot as plt
import numpy as np

x = np.linspace(-5, 5, 50)
z = 1/(1 + np.exp(-x))

plt.subplots(figsize=(8, 5))
plt.plot(x, z)
plt.grid()
plt.show()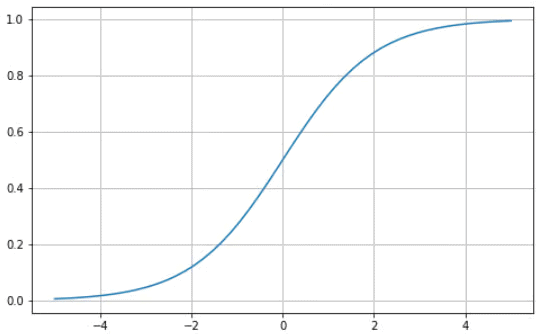

双曲函数

双曲正切 (tanh) 具有与 S 型函数相同的“S”形曲线，只是值在 -1 和 1 之间。因此，较小的输入映射更接近 -1，而较大的输入映射更接近 1。

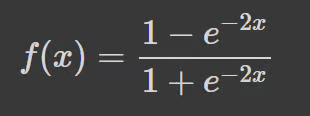
以下是使用 Python 可视化的 tanh 函数示例： 

# tanh function in Python
import matplotlib.pyplot as plt
import numpy as np

x = np.linspace(-5, 5, 50)
z = np.tanh(x)

plt.subplots(figsize=(8, 5))
plt.plot(x, z)
plt.grid()
plt.show()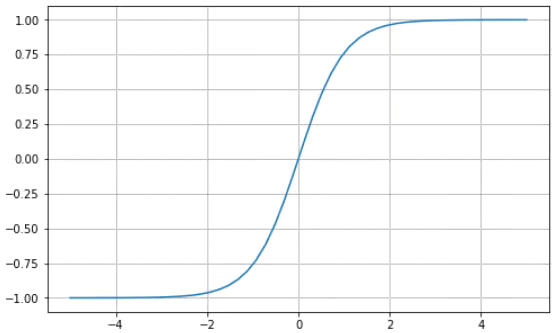

Softmax

softmax 函数通常用作输出层的激活函数。它是 sigmoid 函数在多维上的推广。因此，它在神经网络中用于预测两个以上标签上的类别成员身份。 

整流线性单元 (ReLU)

使用 sigmoid 或 tanh 函数构建深度神经网络是有风险的，因为它们更容易受到梯度消失问题的影响。整流线性单元 (ReLU) 激活函数就是为了解决此问题而出现的，并且通常是多个神经网络的默认激活函数。 

以下是使用 Python 的 ReLU 函数的可视化示例： 

# ReLU in Python
import matplotlib.pyplot as plt
import numpy as np

x = np.linspace(-5, 5, 50)
z = [max(0, i) for i in x]

plt.subplots(figsize=(8, 5))
plt.plot(x, z)
plt.grid()
plt.show()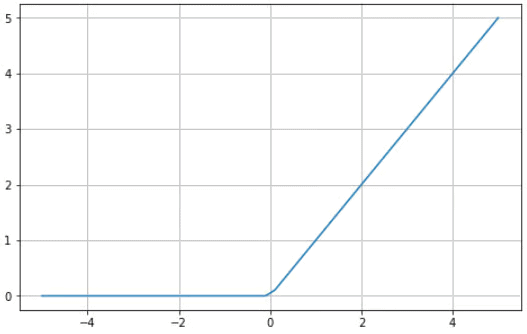

ReLU 的范围在零和无穷大之间：请注意，对于小于或等于零的输入值，该函数返回零，而对于大于零的值，该函数返回提供的输入值（即，如果您输入两个，则将返回两个）。最终，ReLU 函数的行为与线性函数极为相似，这使得它更容易优化和实现。 

从输入层到输出层的过程称为前向传递或正向传播。在此阶段，模型生成的输出用于计算成本函数，以确定神经网络在每次迭代后的表现。然后，此信息通过模型传回以校正权重，从而使模型能够在称为反向传播的过程中做出更好的预测。 

反向传播

在第一次前向传播结束时，网络使用未调整的初始化权重进行预测。因此，模型的预测很可能不准确。利用前向传播计算出的损失，我们将信息传回网络以微调权重，这个过程称为反向传播。 

最终，我们使用优化函数来帮助我们识别可能降低错误率的权重，从而使模型更可靠，并提高其推广到新实例的能力。

PyTorch 教程：从头开始构建神经网络的分步指南

在本文部分中，我们将使用 PyTorch 库构建一个简单的人工神经网络模型。查看此 DataCamp工作区以跟踪代码

PyTorch 是深度学习最受欢迎的库之一。它提供了比 TensorFlow 更直接的调试体验。它还有其他一些优势，例如分布式训练、强大的生态系统、云支持、允许您编写可用于生产的代码等。

让我们进入教程。 

数据定义和准备 

我们将在本教程中使用的数据集是 scikit-learn 中的 make_circles – 请参阅文档。这是一个玩具数据集，包含二维平面上的一个大圆和一个小圆以及两个特征。为了演示，我们使用了 10,000 个样本，并在数据中添加了 0.05 标准差的高斯噪声。 

在构建神经网络之前，最好将数据分成训练集和测试集，以便我们可以评估模型在未知数据上的性能。

import matplotlib.pyplot as plt
from sklearn.datasets import make_circles
from sklearn.model_selection import train_test_split

# Create a dataset with 10,000 samples.
X, y = make_circles(n_samples = 10000,
                    noise= 0.05,
                    random_state=26)

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=.33, random_state=26)

# Visualize the data.
fig, (train_ax, test_ax) = plt.subplots(ncols=2, sharex=True, sharey=True, figsize=(10, 5))
train_ax.scatter(X_train[:, 0], X_train[:, 1], c=y_train, cmap=plt.cm.Spectral)
train_ax.set_title("Training Data")
train_ax.set_xlabel("Feature #0")
train_ax.set_ylabel("Feature #1")

test_ax.scatter(X_test[:, 0], X_test[:, 1], c=y_test)
test_ax.set_xlabel("Feature #0")
test_ax.set_title("Testing data")
plt.show()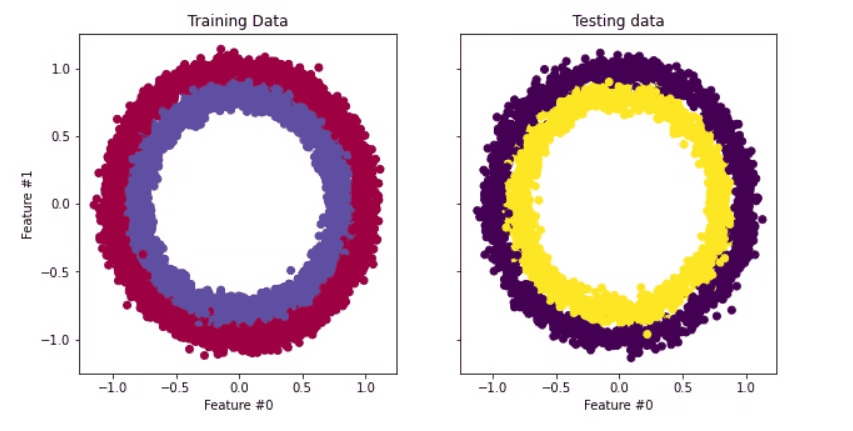

下一步是将训练和测试数据从NumPy 数组转换为PyTorch 张量。为此，我们将为训练和测试文件创建自定义数据集。我们还将利用 PyTorch 的Dataloader模块，以便批量训练数据。代码如下： 

import warnings
warnings.filterwarnings("ignore")

!pip install torch -q

import torch
import numpy as np
from torch.utils.data import Dataset, DataLoader

# Convert data to torch tensors
class Data(Dataset):
    def __init__(self, X, y):
        self.X = torch.from_numpy(X.astype(np.float32))
        self.y = torch.from_numpy(y.astype(np.float32))
        self.len = self.X.shape[0]
       
    def __getitem__(self, index):
        return self.X[index], self.y[index]
   
    def __len__(self):
        return self.len
   
batch_size = 64

# Instantiate training and test data
train_data = Data(X_train, y_train)
train_dataloader = DataLoader(dataset=train_data, batch_size=batch_size, shuffle=True)

test_data = Data(X_test, y_test)
test_dataloader = DataLoader(dataset=test_data, batch_size=batch_size, shuffle=True)

# Check it's working
for batch, (X, y) in enumerate(train_dataloader):
    print(f"Batch: {batch+1}")
    print(f"X shape: {X.shape}")
    print(f"y shape: {y.shape}")
    break

Batch: 1
X shape: torch.Size([64, 2])
y shape: torch.Size([64])

现在让我们继续实现和训练我们的神经网络。 

神经网络实现和模型训练

我们将实现一个使用 ReLU 激活函数 (torch.nn. functional.relu) 的简单两层神经网络。为此，我们将创建一个名为 NeuralNetwork 的类，该类继承自 nn.Module，它是 PyTorch 中内置的所有神经网络模块的基类。 

代码如下： 

import torch
from torch import nn
from torch import optim

input_dim = 2
hidden_dim = 10
output_dim = 1

class NeuralNetwork(nn.Module):
    def __init__(self, input_dim, hidden_dim, output_dim):
        super(NeuralNetwork, self).__init__()
        self.layer_1 = nn.Linear(input_dim, hidden_dim)
        nn.init.kaiming_uniform_(self.layer_1.weight, nonlinearity="relu")
        self.layer_2 = nn.Linear(hidden_dim, output_dim)
       
    def forward(self, x):
        x = torch.nn.functional.relu(self.layer_1(x))
        x = torch.nn.functional.sigmoid(self.layer_2(x))

        return x
       
model = NeuralNetwork(input_dim, hidden_dim, output_dim)
print(model)


"""
NeuralNetwork(
  (layer_1): Linear(in_features=2, out_features=10, bias=True)
  (layer_2): Linear(in_features=10, out_features=1, bias=True)
)

就这样。 

为了训练模型，我们必须定义一个用于计算梯度的损失函数和一个用于更新参数的优化器。为了演示，我们将使用二元交叉熵和随机梯度下降，学习率为 0.1。 

learning_rate = 0.1

loss_fn = nn.BCELoss()

optimizer = torch.optim.SGD(model.parameters(), lr=lea

让我们训练我们的模型

num_epochs = 100
loss_values = []


for epoch in range(num_epochs):
    for X, y in train_dataloader:
        # zero the parameter gradients
        optimizer.zero_grad()
       
        # forward + backward + optimize
        pred = model(X)
        loss = loss_fn(pred, y.unsqueeze(-1))
        loss_values.append(loss.item())
        loss.backward()
        optimizer.step()

print("Training Complete")

Training Complete

由于我们跟踪了损失值，我们可以直观地看到模型随时间的损失。 

step = range(len(loss_values))

fig, ax = plt.subplots(figsize=(8,5))
plt.plot(step, np.array(loss_values))
plt.title("Step-wise Loss")
plt.xlabel("Epochs")
plt.ylabel("Loss")
plt.show()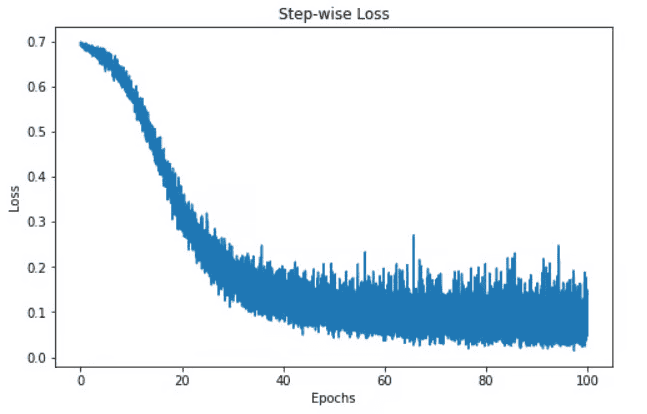

上面的可视化显示了我们的模型在 100 个 epoch 中的损失。最初，损失从 0.7 开始逐渐减小 – 这表明我们的模型一直在随着时间的推移改进其预测。然而，该模型似乎在 60 个 epoch 左右趋于稳定，这可能是由多种原因造成的，例如模型可能处于损失函数的局部或全局最小值区域。 

尽管如此，该模型已经过训练并准备对新实例进行预测 – 让我们在下一节中看看如何做到这一点。

预测和模型评估

使用我们的 PyTorch 神经网络进行预测非常简单。 

import itertools  # Import this at the top of your script

# Initialize required variables
y_pred = []
y_test = []
correct = 0
total = 0

"""
We're not training so we don't need to calculate the gradients for our outputs
"""
with torch.no_grad():
    for X, y in test_dataloader:
        outputs = model(X)  # Get model outputs
        predicted = np.where(outputs.numpy() < 0.5, 0, 1)  # Convert to NumPy and apply threshold
        predicted = list(itertools.chain(*predicted))  # Flatten predictions
        y_pred.append(predicted)  # Append predictions
        y_test.append(y.numpy())  # Append true labels as NumPy
        total += y.size(0)  # Increment total count
        correct += (predicted == y.numpy()).sum().item()  # Count correct predictions

print(f'Accuracy of the network on the 3300 test instances: {100 * correct // total}%')

Accuracy of the network on the 3300 test instances: 97%

注意：每次运行代码都会产生不同的输出，因此您可能无法获得相同的结果。 

上述代码循环遍历存储在 test_dataloader 变量中的测试批次，而不计算梯度。然后，我们预测批次中的实例，并将结果存储在名为输出的变量中。接下来，我们确定将所有小于 0.5 的值设置为 0，将等于或大于 0.5 的值设置为 1。然后将这些值附加到我们的预测列表中。

之后，我们将批次中实例的实际预测添加到名为 total 的变量中。然后，我们通过确定与实际类别相等的预测数量并将它们相加来计算正确预测的数量。每个批次的正确预测总数都会增加并存储在我们的正确变量中。

为了计算整个模型的准确率，我们将正确预测的数量乘以 100（得到百分比），然后除以测试集中的实例数量。我们的模型准确率为 97%。我们使用混淆矩阵和 scikit-learn 的分类报告进一步深入研究，以更好地了解我们的模型的表现。

from sklearn.metrics import classification_report
from sklearn.metrics import confusion_matrix

import seaborn as sns

y_pred = list(itertools.chain(*y_pred))
y_test = list(itertools.chain(*y_test))

print(classification_report(y_test, y_pred))

"""
              precision    recall  f1-score   support

        0.0       0.98      0.97      0.98      1635
        1.0       0.98      0.98      0.98      1665

    accuracy                           0.98      3300
  macro avg       0.98      0.98      0.98      3300
weighted avg       0.98      0.98      0.98      3300

"""

cf_matrix = confusion_matrix(y_test, y_pred)

plt.subplots(figsize=(8, 5))

sns.heatmap(cf_matrix, annot=True, cbar=False, fmt="g")

plt.show()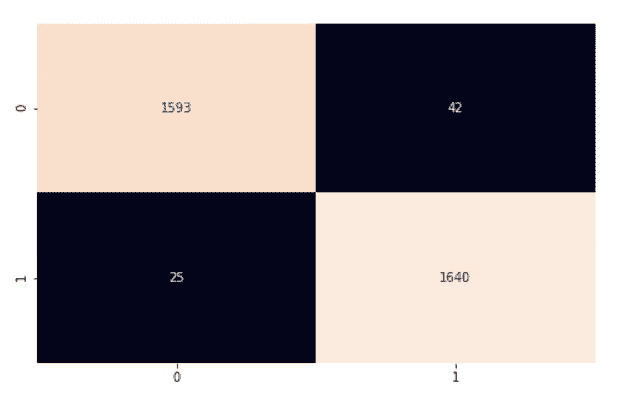

我们的模型表现相当不错。我鼓励您探索代码并进行一些更改，以帮助实现我们在本文中介绍的内容。  

在本 PyTorch 教程中，我们介绍了神经网络的基本知识，并使用 PyTorch（一个用于深度学习的 Python 库）来实现我们的网络。我们使用来自 scikit-learn 的圆形数据集来训练两层神经网络进行分类。然后，我们对数据进行预测，并使用准确度指标评估结果。